Το πρόβλημα του καναπέ! (Sofa problem)

 

    
Το 1966,ο Aυστριακός μαθηματικός Leo Moser έθεσε ένα ευφάνταστο όσο και  πρακτικό ερώτημα:

  Έστω ένας διάδρομος με 1 μέτρο πλάτος, ποιο θα είναι το σχήμα και οι διαστάσεις  του μεγαλυτέρου καναπέ που θα μπορούσε  να "περάσει" από μια γωνία  αυτού του διάδρομου; Ουσιαστικά το πρόβλημα προβάλλει στις δυο διαστάσεις  ένα ζήτημα μεταφοράς επίπλου( καναπέ) του πραγματικού κόσμου.Το ερώτημα είναι να βρεθούν οι ακριβείς διαστάσεις  του μεγαλύτερου επιπέδου σχήματος εμβαδού Α ώστε να μπορεί να «περάσει» μέσα από ένα διάδρομο σχήματος L με πλάτος  1 μονάδα μήκους.Το εμβαδό Α  του μεγίστου σχήματος ονομάζεται σταθερά του καναπέ (sofa Constant).
 Όλα αυτά πριν από 46 χρόνια, όπου παραμένει ένα ανοικτό πρόβλημα.Το 1968, ο Βρετανός John Michael Hammersley έδειξε ότι ένας καναπές σε σχήμα  ακουστικού τηλεφώνου θα μπορούσε να «περάσει» την γωνία του διαδρόμου,ακόμη και αν το εμβαδό του είναι μεγαλύτερο από  2 τετραγωνικά μέτρα (δείτε το σχήμα).                                  


                             

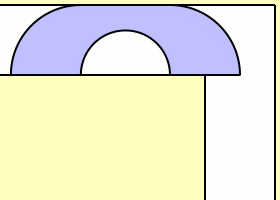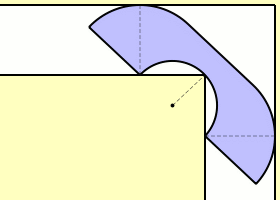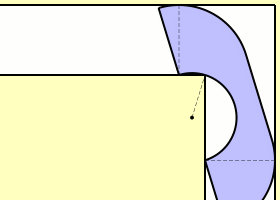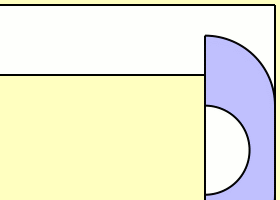
Η σταθερά του καναπέ  (sofa Constant) σύμφωνα με τον Hammersley είναι  μεγαλύτερη  από 2.207416099. Το 1992,ο Joseph Gerver βελτίωσε την προσέγγιση του Hammersley,  βρήκε ένα μεγαλύτερο κάτω  άκρο της σταθεράς τον αριθμό 2.219531669.Το πρόβλημα όμως παραμένει ανοικτό.

                       

Σχετικά προβλήματα  51-52 σελ 73-74  στη "χήρα με τα προβλήματα για την Γ Λυκείου" στο σύνδεσμο (https://drive.google.com/file/d/1VK0GeKhoAthgrXlddxffy9ipGJSqWYFc/view)

Σχετικοί σύνδεσμοι:

http://mathworld.wolfram.com/MovingSofaProblem.html

http://cs.utsa.edu/~wagner/pubs/corner/corner_final.pdf