Σαν σήμερα 25 Ιανουαρίου στο μαθηματικό σύμπαν

  Επαναφορά στα geek ενδιαφέροντα του ιστολογίου. Σταχυολόγηση γεγονότων που έλαβαν χώρα στις 25 Ιανουαρίου και αφορούν έμμεσα ή άμεσα το μαθηματικό σύμπαν.

  1736.Γεννιέται ο Γάλλο-ιταλός μαθηματικός Joseph-Louis de Lagrange,με σημαντικό έργο  στην θεωρία  αριθμών,την μαθηματική ανάλυση και την μηχανική.Καθολική  ευφυΐα,  σαν μαθητής στο σχολείο έδειχνε μεγαλύτερο ενδιαφέρον για τα κλασικά μαθήματα και  μάλλον από τύχη ακολούθησε τα μαθηματικά. Στα πλαίσια των κλασσικών μελετών ήρθε σε επαφή με τις εργασίες του Ευκλείδη και του Αρχιμήδη που τον εντυπωσίασαν.Κατόπιν έπεσε στα χέρια του ένα δοκίμιο  του Halley για την ανωτερότητα του απειροστικού λογισμού έναντι των συνθετικών γεωμετρικών  μεθόδων των αρχαίων Ελλήνων.'Εκτοτε,έγινε ένας ζηλωτής της μαθηματικής  ανάλυσης και γρήγορα την έκανε κτήμα του. Ο θρύλος τον θέλει σε ηλικία 18 ετών να γίνεται καθηγητής μαθηματικών στην σχολή πυροβολικού στο Τορίνο.Πάντα αναλύστας και ποτέ γεωμέτρης  για το αριστούργημα του Αναλυτική μηχανική (Mécanique analytique ,1788) έλεγε χιουμοριστικά: «..δεν θα βρείτε διαγράμματα σε αυτήν την εργασία..». Tελειομανής, γράφει στον φίλο του D Alempert «Καθώς δεν πιέζομαι  και εργάζομαι περισσότερο από ευχαρίστηση παρά από καθήκον , μοιάζω με τους θεούς που  κτίζουν:κατασκευάζω ,χαλώ και ξανακατασκευάζω , μέχρι που να μείνω σχετικά ικανοποιημένος με το αποτέλεσμα,πράγμα που συμβαίνει σπάνια.» 

Πέθανε σε ηλικία 76 ετών.(Bell ,1965)

1812.Γεννιέται ο Άγγλος μαθηματικός William Shanks ,ο οποίος έμεινε στην ιστορία κυρίως για την εργασία του στον υπολογισμό ψηφιών του π.Το 1812 ,δεν υπήρχαν υπολογιστές.Δάσκαλος σε ένα σχολείο στην περιοχή του Durham,υπολόγισε  703 ψηφία του π με την χρήση του τύπου:

                                            π/4 = 4 tan^(-1)[(1/5)] - tan(-1)[(1/239)]   
 Δυστυχώς,το 1944, διαπιστώθηκε με νέο υπολογισμό ότι ο Shanks είχε κάνει λάθος στο  528^ο  ψηφίο και φυσικά και στα υπόλοιπα από εκεί και πέρα.

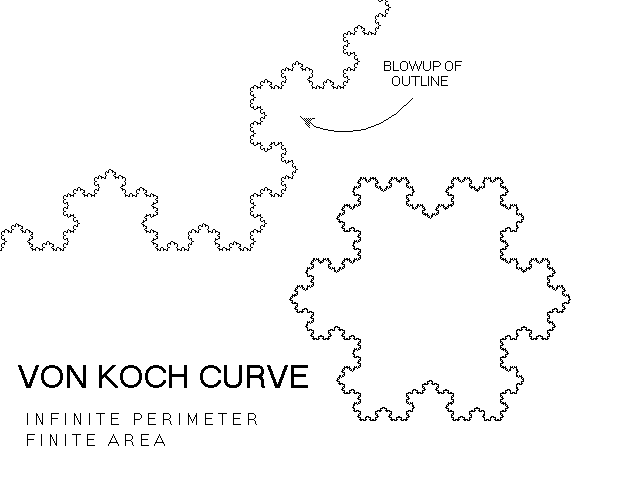
1870.Γεννιέται ο Σουηδός μαθηματικός Niels Fabian Helge von Koch,έδωσε το όνομα του στο διάσημο φράκταλ γνωστό ως Koch snowflake ,ίσως ένα από τα πρώτα φράκταλ που ανακαλύφθηκαν.

                          

   Ο  Von Koch ασχολήθηκε επισταμένα με την θεωρία αριθμών.Το 1901 ,απέδειξε  ότι η εικασία Riemann  είναι ισοδύναμη με  μια ισχυρότερη μορφή  του θεωρήματος  πρώτων αριθμών (prime number theorem  https://en.wikipedia.org/wiki/Prime_number_theorem)

Ο ίδιος περιγράφει την καμπύλη Koch  σε μια δημοσίευση ,το 1904 με τίτλο: «Μια συνεχής καμπύλη  χωρίς εφαπτομένες  που κατασκευάζεται με στοιχειώδη γεωμετρία»

(Sur une courbe continue sans tangente, obtenue par une construction géométrique élémentaire)

 Κλικ  εδώ για να δείτε  πως κατασκευάζεται η καμπύλη Koch

1931.Ο διακεκριμένος φυσικός Max Planck ,δηλώνει στο περιοδικό  Observer:

«Θεωρώ την συνείδηση θεμελιώδη. Θεωρώ την ύλη παράγοντα της συνείδησης. Δεν μπορούμε να πάμε πέρα από την συνείδηση. Για οτιδήποτε μιλάμε, οτιδήποτε αντιλαμβανόμαστε ως αληθινό προϋποθέτει να υπάρχει συνείδηση.»

1955. Επιστήμονες  του πανεπιστημίου Columbia  κατασκεύασαν το πρώτο ατομικό ρολόι  τόσο ακριβές  που αποκλίνει μόνο  ένα δευτερόλεπτο κάθε 300 χρόνια. 

                            

 1973.Πεθαίνει στο Νορβηγικό Όσλο, ο διακεκριμένος μαθηματικός  Wilhelm Ljunggren, διέπρεψε στην  θεωρία  αριθμών και ειδικότερα στις  διοφαντικές εξισώσεις. Απέδειξε ότι η εξίσωση:

                                                    X² =2Y⁴ − 1
έχει μόνο δυο ακέραιες λύσεις (1,1), (239,13) ,η εξίσωση έκτοτε φέρει το όνομα του.

Σε μια κλασική περίπτωση μαθηματικής πολυγένεσης,το 1943 έθεσε το ερώτημα  για τις ακέραιες λύσεις της εξίσωσης:

                                                   2ⁿ − 7 = x²

πρόβλημα το οποίο είχε πραγματευτεί ανεξάρτητα και ο θρυλικός Ramanoytzan  30 χρόνια νωρίτερα. Η  παραπάνω εξίσωση φέρει το όνομα Ramanujan–Nagell

 

Wilhelm Ljunggren (7 October 1905 – 25 January 1973)

 

1979. (geek)Λαμβάνει χώρα το πρώτο περιστατικό παραβίασης του πρώτου νόμου του Ισαάκ Ασιμοφ για τα ρομπότ.«Το ρομπότ δε θα κάνει κακό σε άνθρωπο, ούτε με την αδράνειά του θα επιτρέψει να βλαφτεί ανθρώπινο όν.» Ο  εικοσιπεντάχρονος Robert Williams από το  Michigan των Η.Π.Α χάνει την ζωή του από ένα ρομπότ. Έργαζοταν σε εργοστάσιο της Ford και ο βραχίονας του ρομπότ τον χτύπησε στο κεφάλι σκοτώνοντας τον ακαριαία, αποδείχτηκε ότι δεν υπήρχαν μηχανισμοί ασφαλείας.

2013.Στις 25 Ιανουαρίου,ο Dr. Curtis Cooper  από το πανεπιστήμιο του Missouri ανακάλυψε  το 48^ο  πρώτο  αριθμό Mersenne, 2^57,885,161-1, ένα αριθμό με 17425170 ψηφία.Η  Helen Arney (αυτοπροσδιορίζεται ως Musical comedian.Geek Songstress) έγραψε ένα μικρό χριστουγεννιάτικο τραγούδι  που το ονόμασε Mersenne 48.(Εμείς εδώ, μόνο πιάτα στην Πάολα  ξέρουμε να πετάμε.) Στην ηλεκτρονική  διεύθυνση.

               http://helenarney.bandcamp.com/track/bonus-track-mersenne-48

Το 2016 ανακαλύφθηκε ο  49^ο  πρώτος Mersenne.

  

                        ]

  Bonus, μια ψευδοαπόδειξη.
Ο Lagrange μεταξύ άλλων απέδειξε και το θεώρημα:
Αν o p είναι πρώτος αριθμός τότε και ο αριθμός  1*2*3*...*(p-1) - 1 είναι πρώτος.
Για παράδειγμα,αν p=7 τότε 1*2*3*4*5*6-1=719  που είναι πρώτος αριθμός.
Ένας Ισπανός ευγενής(σύγχρονος  του Lagrange)  για το παραπάνω θεώρημα έδωσε την εξής ψευδοαπόδειξη:
 Ισχύει:
(p-1) + 1 =p   βάζουμε και στα δυο μέλη θαυμαστικό ( το σύμβολο για το παραγοντικό)

(p-1)! + 1! =p!

1*2*3*...*(p-1) + 1 =p το δεύτερο μέλος είναι πρώτος αριθμός αρα και το πρώτο!!!!
(Bell,1965)