..Τους ζήτησε να πάρουν τον κόκκινο μαρκαδόρο και να γράψουν στο πίνακα μπλε,η τάξη στην αρχή ήταν αμήχανη,πως στην ευχή,μπορείς με ένα κόκκινο μαρκαδόρο να γράψεις μπλε;;Πήρε τον μαρκαδόρο και έγραψε στον πίνακα «μπλε»...
Αλι Νταρ Νασάθ, "Η σχολική τάξη"
Πιστός στην άποψη ότι, αυτό που μετράει είναι το ταξίδι και όχι ο προορισμός ανέκαθεν με ενδιέφερε η διαδικασία επίλυσης ενός μαθηματικού προβλήματος.Η ανάλυση βήμα- βήμα της λύσης μιας άσκησης ή ενός προβλήματος βοήθα τους μαθητές να «χαρτογραφούν» την πορεία για την λύση αλλά παράλληλα και να αποσαφηνίσουν την θεωρία.Οι περισσότεροι μαθητές για την επίλυση ασκήσεων ή προβλημάτων βασίζονται σε παλιότερα ανάλογα προβλήματα με αυτά που τους τίθενται ,μέθοδος εξαιρετικά χρήσιμη αλλά πολλές φορές ανεπαρκής.H κατηγοριοποίηση μεθοδολογιών αποτελεί μοναδικό εργαλείο για την επίλυση ασκήσεων αλλά όσο αφορά τα μαθηματικά προβλήματα είναι τροχοπέδη. Ουσιαστικά πρόκειται για μονοδρόμηση της μαθηματικής σκέψης, κατάσταση όμως που στερεί από τον μαθητή , την δυνατότητα αναπτύσσοντας πρωτοβουλίες να αντιμετωπίζει επιτυχώς μαθηματικές καταστάσεις που βλέπει για πρώτη φορά. Στην παρούσα ανάρτηση θα δούμε πως κάποιες φορές για τον επιτυχή χειρισμό ενός μαθηματικού προβλήματος αρκεί να υιοθετήσουμε μια νέα οπτική.
Ας δούμε ένα κλασσικό παράδειγμα με δυο διαφορετικές στην φιλοσοφία προσεγγίσεις .
Ας δούμε ένα κλασσικό παράδειγμα με δυο διαφορετικές στην φιλοσοφία προσεγγίσεις .
« Ο Κώστας εξετάζεται σε ένα τεστ,το τεστ αποτελείται από 20 ερωτήματα.Κάθε σωστή απάντηση πριμοδοτείται με 5 μονάδες,για κάθε λάθος απάντηση αφαιρούνται 2 μονάδες , ενώ για τα ερωτήματα που δεν απαντήθηκαν δεν δίνονται μονάδες. Γνωρίζουμε ότι ο Κώστας συγκέντρωσε 44 μονάδες και δεν απάντησε σε κάποια ερωτήματα. Να βρεθούν πόσα ερωτήματα απαντήθηκαν σωστά , πόσα ερωτήματα απαντήθηκαν λάθος , τέλος το πλήθος των ερωτημάτων που δεν απαντήθηκαν.»
Πως θα χειριζόμασταν το πρόβλημα αλγεβρικά;
Θα λέγαμε έστω:
Χ:το πλήθος των ερωτημάτων που απαντήθηκαν σωστά
Υ: το πλήθος των ερωτημάτων που απαντήθηκαν λανθασμένα.
Ζ: το πλήθος των ερωτημάτων δεν που απαντήθηκαν .
Από τα δεδομένα του προβλήματος προκύπτει;
X+Y+Z=20 (1)
5X-2Y+0Z=44 η 5X-2Y=44 (2)
Λύνουμε την (1) ως προς Υ και αντικαθιστούμε στην (2) και προκύπτει η εξίσωση:
7Χ+2Ζ=84 (3) ή Ζ=(84-7Χ)/2
Γνωρίζουμε ότι ο Ζ είναι θετικός ακέραιος τότε ο Χ πρέπει να είναι άρτιος και τουλάχιστον 10 για να μπορέσουμε να έχουμε ένα άθροισμα βαθμών 44.( το ότι είναι άρτιος ο Χ το συμπεραίνουμε από τον παρανομαστή του κλάσματος που είναι 2 άρα ο αριθμητής πρέπει να είναι πολλαπλάσιο του 2 για να προκύπτει ο Ζ θετικός ακέραιος ) .
Άρα 84-7X πολ/σιο του 2 ,Χ μεγαλύτερο η ισο του 10.
Οι παραπάνω προϋπόθεση μας οδηγεί στον παρακάτω πίνακα με όλες τις δυνατές περιπτώσεις:
Χ
|
10
|
12
|
14
|
Y
|
3
|
8
|
13
|
Z
|
7
|
0
|
-7
|
Το Ζ δεν μπορεί να είναι αρνητικός ούτε μηδέν (είναι σαφές από την εκφώνηση ότι ο Κώστας δεν απάντησε σε κάποια ερωτήματα) . Άρα η μοναδική λύση είναι Χ=10,Ζ=7,Y=3.
Η παραπάνω λύση απαιτεί αλγεβρικό χειρισμό. Ας δούμε μια διαφορετική προσέγγιση όπου κάνοντας τις σωστές ερωτήσεις και «μαντεύοντας έξυπνα» θα λύσουμε το πρόβλημα πιο κομψά ( όσο αδόκιμος και αν είναι ο ορός ).
Πόσα ερωτήματα απάντησε σωστά ο Κώστας ; Πρέπει να είναι τουλάχιστον 10 διότι αν είχε απαντήσει μόνο 9 σωστά , θα είχε μια συμβολική βαθμολογία 9x5=45 και όσα λάθος ερωτήματα και αν απαντήσει η συνολική αρνητική βαθμολογία θα ήταν πολλαπλάσιο του 2 άρα αποκλείεται να αφαιρέσουμε από το 45 οποιοδήποτε πολλαπλάσιο του 2 και να καταλήξουμε στο 44.Οποτε είναι βέβαιο ότι τα σωστά ερωτήματα είναι από 10 και πάνω.
Aν ήταν ακριβώς 10 τότε ο Κώστας θα είχε 3 λάθος ερωτήματα , 7 ερωτήματα που δεν απαντήθηκαν και θα καταλήγαμε στην βαθμολογία των 44 βαθμών. Αυτή είναι μια σωστή απάντηση ,είναι όμως η μοναδική;
Ας υποθέσουμε ότι ο Κώστας απάντησε σωστά 11 ερωτήματα τότε θα είχε μια βαθμολογία από τις σωστές απαντήσεις 11x5=55 βαθμούς .Αφαιρώντας όμως οποιοδήποτε πολλαπλάσιο του 2 ( που είναι πάντα η συνολική αρνητική βαθμολογία) δεν θα καταλήγαμε στο 44. Άρα αποκλείεται το πλήθος των σωστών ερωτημάτων να είναι 11.
Ας δοκιμάσουμε το 12 τότε 5x12=60 τότε 60- 16 =44 , αυτό σημαίνει ότι είχε 12 σωστά ,8 λάθος και κανένα ερώτημα που να μην απαντήθηκε . Ωστόσο, αυτό είναι άτοπο γιατί γνωρίζουμε ότι υπάρχουν και ερωτήματα που δεν απαντήθηκαν. Το 13 απορρίπτεται για τον ίδιο λόγο που απορρίφτηκε το 11.
Συνεχίζουμε απορρίπτοντας κάθε τιμή από το 12 και μετά.( Η μέγιστη βαθμολογία που μπορεί να επιτευχθεί είναι 100 βαθμοί) Άρα η μοναδική λύση είναι 10,7,3.
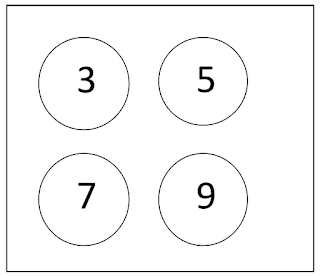
Ας δούμε ένα δεύτερο παράδειγμα που η προφανής λύση είναι χρονοβόρα και για θα πρέπει να υιοθετήσουμε μια άλλη « οπτική». Ένα κουτί περιέχει 4 σφαίρες, Σε κάθε σφαίρα είναι γραμμένος ένας από τους αριθμούς 3,5,7,9 .
Επιλέγουμε τυχαία μια- μια τις σφαίρες από το κουτί και τοποθετούμε τις σφαίρες που επιλέγουμε από τα αριστερά προς τα δεξιά . Ποια είναι η πιθανότητα ο τετραψήφιος αριθμός που θα προκύψει να είναι πρώτος ( διαιρείται μόνο με τον εαυτό του και την μονάδα).
Οι περισσότεροι μαθητές βλέποντας το πρόβλημα ,καταγράφουν όλες τις δυνατές περιπτώσεις επιλογής και ελέγχουν σε ποια περίπτωση ο αριθμός που προκύπτει είναι πρώτος .
3579 5379 7953 9573
3597 5397 7935 9535
3759 5739 7395 9573
3595 5793 7359 9537
3975 5973 7539 9357
3957 5793 7593 9375
Αν κάνουμε σωστά τους υπολογισμούς θα οδηγηθούμε στην απάντηση. Αλλά η διαδικασία είναι εξαιρετικά χρονοβόρα. Για ένα τετραψήφιο αριθμό , για να ελέγξουμε αν είναι πρώτος πρέπει να κάνουμε στην χειρότερη των περιπτώσεων 500 διαιρέσεις και οι αριθμοί είναι 24,αυτό μας οδηγεί στο συμπέρασμα ότι πρέπει να υπάρχει και άλλος τρόπος . Ας προσπαθήσουμε να δούμε το πρόβλημα με «άλλο μάτι». Τα ψηφία όλων αυτών των αριθμών είναι τα 3,5,7 και 9.Το άθροισμα τους είναι :3+5+7+9=24 αριθμός πολλαπλάσιο του 3 άρα σίγουρα ο καθένας από τους αριθμούς είναι πολλαπλάσιο του 3 οπότε σίγουρα δεν είναι πρώτος. Οπότε η πιθανότητα ένας τουλάχιστον από τους αριθμούς να είναι πρώτος είναι μηδενική.
(Περισσότερα για τα κριτήρια διαιρετότητας: ΠΑΤΗΣΕ ΕΔΩ)
(Περισσότερα για τα κριτήρια διαιρετότητας: ΠΑΤΗΣΕ ΕΔΩ)

Καλησπέρα!!
ΑπάντησηΔιαγραφήΕξαιρετικά ενδιαφέροντα όσα υπάρχουν στο ιστολόγιο σας!
Εχω όμως μια απορία :
Πως καταλήξατε τόσο εύκολα, απλά και μόνο από το συμπέρασμα οτι κανενα απο τα "μέλη"-αριθμοι των αλληλουχιων, δεν ειναι πρωτος, στο ότι και καμία απ΄οτις αλληλουχίες δεν είναι πρώτος αριθμοος;
:/
Καλό σας βράδυ :)
Δεν συμπεραίνουμε ότι όλοι οι τετραψήφιοι που κατασκευάζονται από τα ψηφία 3,5,9,7 είναι πρώτοι επειδή το καθένα από τα ψηφία αυτά είναι πρώτος . Γνωρίζουμε ότι ένας αριθμός είναι πολλαπλάσιο του 3 αρκεί το άθροισμα των ψηφίων του να είναι πολλαπλάσιο του 3 .Για παράδειγμα, ο 225 , μπορούμε να διαπιστώσουμε αν είναι πολλαπλάσιο του 3 χωρίς να κάνουμε την διαίρεση, προσθέτουμε τα ψηφία του αριθμού 2+2+5=9, το 9 είναι πολλαπλάσιο του 3 άρα και το 225 θα είναι πολλαπλάσιο του 3. Στο συγκεκριμένο πρόβλημα , οποιοσδήποτε τετραψήφιος αποτελείται από τα 3,5,7,9 έχει άθροισμα ψηφίων 3+5+7+9=24 ( 24 πολλαπλάσιο του 3) άρα και το 3 είναι διαιρέτης του αριθμού οπότε αποκλείεται να είναι πρώτος.
ΑπάντησηΔιαγραφή