Ένας μαθηματικός τύπος που "αναπαράγει" τον εαυτό του! (Tupper’s self-referential formula)

                                                    

   Ο αυτοαναφορικός τύπος του Tupper (Tupper’s self-referential formula) είναι μια ανισοτική σχέση με δυο μεταβλητές x,y  που όταν παρασταθεί γραφικά σε ένα σύστημα συντεταγμένων  αναπαράγει οπτικά την ίδια την ανισοτικη σχέση .Η σχέση ειναι :
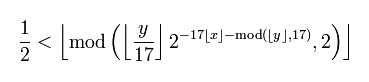                               (1)
όπου [.] ειναι η συνάρτησή ακέραιο μέρος και mod είναι ο αριθμητικός τελεστής που υπολογίζει το ακέραιο υπόλοιπο μιας διαίρεσης δυο ακέραιων αριθμών.Με  κ να είναι η σταθερά:

48584506361897134235820959624942020445814005879832445494830930850619
34704708809928450644769865524364849997247024915119110411605739177407
85691975432657185544205721044573588368182982375413963433822519945219
16512843483329051311931999535024137587652392648746133949068701305622
95813219481113685339535565290850023875092856892694555974281546386510
73004910672305893358605254409666435126534936364395712556569593681518
43348576052669401612512669514215505395545191537854575257565907405401
57929001765967965480064427829131488548259914721248506352686630476300

 Το σύνολο των σημείων (x,y-k) με  0<=χ<=105 και κ<=y<κ+16  και  που ικανοποιούν τη σχέση (1)      δίνει το ακολουθο γράφημα που ειναι "κλώνος" του τύπου του Tupper

                         
Ο Jeffee Tupper ανακαλυψε τον τυπο το 2001 και χρησιμοποιησε για την γραφικη απεικονιση του το προγραμμα  GrafEq .

 Γραφικη απεικονιοση του τυπου το Tupper  σε Java
 http://web.aanet.com.au/superseed/ajmcrae/TupperPlot/TupperPlot.html

 Περισσοτερα στα link
http://www.dgp.toronto.edu/people/mooncake/papers/SIGGRAPH2001_Tupper.pdf

http://shreevatsa.wordpress.com/2011/04/12/how-does-tuppers-self-referential-formula-work/

http://mathworld.wolfram.com/TuppersSelf-ReferentialFormula.html


Σχετικό βίντεο από τον διαδικτυακό μαθηματικό κανάλι Numberphile